Persistent hubs in weighted graphs
Mattia G. Bergomi
Repository gitlab.com/mattia.bergomi/perscomb



Who we are
 Massimo Ferri1
Massimo Ferri1
 Antonella Tavaglione1
Antonella Tavaglione1
 Pietro Vertechi2
Pietro Vertechi2
 Lorenzo Zuffi1
Lorenzo Zuffi1
1 University of Bologna - Bologna, Italy
2 Champalimaud Research - Lisbon, Portugal
Outline
Persistence on weighted graphs
- (Classic) topological persistence
- Combinatorial persistence: Coherent sampling and property-based filters
Applications
- Hubs detection
- Dynamical hubs detection
(Classic) topological persistence
Framework
$\mathbb{X}$ triangulable manifold, $f$ continuous. $\mathbb{X}_{i} = f^{-1}\left(\left(-\infty, a_i\right]\right)$ $$ \mathbb{X}_{1} \subseteq \cdots \subseteq \mathbb{X}_{n} = \mathbb{X} $$
(Classic) topological persistence
Framework
(Classic) topological persistence
Weighted graphs ...
$$ G = \left(V, E \right), \ \ f: E\rightarrow\mathbb{R} $$(Classic) topological persistence
... as simplicial complexes
(Classic) topological persistence
... as simplicial complexes
(Classic) topological persistence
References
D.S. Bassett, and O. Sporns. Network neuroscience. Nature neuroscience, 20.3: 353, 2017.
M. W. Reimann, M. Nolte, M. Scolamiero, K. Turner, R. Perin, G. Chindemi, P. Dlotko, R. Levi, K. Hess, and H. Markram. Cliques of neurons bound into cavities provide a missing link between structure and function}. Frontiers in Computational Neuroscience, 2017.
W. Huang and A. Ribeiro. Persistent homology lower bounds on high-order network distances. IEEE Transactions on Signal Processing, 2017.
S. Pal, T. J. Moore, R. Ramanathan, and A. Swami. Comparative topological signatures of growing collaboration networks. In Workshop on Complex Networks CompleNet, 2017.
G. Petri, P. Expert, F. Turkheimer, R. Carhart-Harris, D. Nutt, P. J. Hellyer, and F. Vaccarino. Homological scaffolds of brain functional networks. Journal of The Royal Society Interface, 2014.
D. Horak, S. Maletic, and M. Rajkovic. Persistent homology of complex networks. Journal of Statistical Mechanics: Theory and Experiment, 2009.
Combinatorial persistence
Questions:
Is it reasonable to speak about persistence and not about homology?
How general can such a framework be?
Combinatorial persistence
Natural pseudodistance
Let $(G, f), (G^\prime, f^\prime)$ be weighted graphs and $H$ the set of isomorphisms from $G$ to $G^\prime$.
The natural pseudodistance of $(G, f)$ and $(G^\prime, f^\prime)$ is
$$ \delta\left(\left(G, f\right), \left(G', f'\right)\right) = \left\{ \begin{array}{l l} \infty & \mbox{if} \ \ \ H=\emptyset \\ \inf_{\phi\in H}\sup_{e\in E} \left|f\left(e\right) - f'\left(\phi\left(e\right)\right)\right| \ \ & \mbox{otherwise} \end{array} \right. $$
Ferri, Massimo. Persistent topology for natural data analysis-A survey. Towards Integrative Machine Learning and Knowledge Extraction. Springer, Cham, 2017. 117-133.
Cagliari, Francesca, Barbara Di Fabio, and Claudia Landi. The natural pseudo-distance as a quotient pseudo-metric, and applications. Forum Mathematicum. Vol. 27. No. 3. De Gruyter, 2015.
d'Amico, Michele, Patrizio Frosini, and Claudia Landi. Natural pseudo-distance and optimal matching between reduced size functions. Acta applicandae mathematicae 109.2 (2010): 527-554.
Combinatorial persistence
Persistence functions
All functions $\lambda_{(G, f)}: \Delta^+ \to \mathbb{Z}$ are said to be persistence functions if
- $\lambda_{(G, f)}(u, v)$ is nondecreasing in $u$ and nonincreasing in $v$ ;
- for all $u_1, u_2, v_1, v_2 \in\mathbb{R}$ such that $u_1 \le u_2 < v_1 \le v_2$ the following inequality holds: $$\lambda_{(G, f)}(u_2, v_1) - \lambda_{(G, f)}(u_1, v_1) \ge \lambda_{(G, f)}(u_2, v_2) - \lambda_{(G, f)}(u_1, v_2)$$
Combinatorial persistence
Stability
$\lambda_{(G, f)}$ is said to be stable if given an analogous pair $(G^\prime, f^\prime)$, an isomorphism $\psi:G\to G^\prime$ exists such that $$\sup_{e\in E} \left| f\left(e \right)-f^\prime\left(\psi\left(e\right)\right)\right|\le h$$ where $h>0$, then for all $(u, v)\in \Delta^+$ the inequality $$\lambda_{(G, f)}(u-h, v+h)\le \lambda_{\left(G^\prime, f^\prime\right)}(u, v)$$ holds.
Combinatorial persistence
A note on stability...
For weighted graphs $\left(G, f\right), \left(G^\prime, f^\prime\right)$ as above, if $\lambda_{(G, f)}$ and $\lambda_{\left(G^\prime, f^\prime\right)}$ are stable then
$$ d\left(D\left( f \right), D\left(f^\prime\right)\right) \le \delta\left(\left(G, f\right), \left(G^\prime, f^\prime\right)\right), $$ where $d$ is the bottleneck distance.
... and a remark on universality
Is the inequality described above the best one that we can obtain from persistence diagrams?
Combinatorial persistence
Coherent samplings
A coherent sampling $\mathcal{V}$ is the assignment to each graph $G$, where $G=\left(V, E\right)$ of a set $\mathcal{V}(G)$ of subsets of $V \cup E$, such that
- each $\mathcal{V}(G)$ is a finite (possibly empty) set of elements of $V\cup E$;
- if $G$ is a subgraph of $H$, then each element of $\mathcal{V}(G)$ is contained in exactly one element of $\mathcal{V}\left(H\right)$;
A coherent sampling is stable if $\psi:G\to G^\prime$ is an isomorphism, then $\mathcal{V}\left(G^\prime\right)=\psi\left(\mathcal{V}\left(G\right)\right)$.
For each inclusion $\iota: G \to H$ let $\Lambda(\iota)$ be the number of elements of $\mathcal{V}\left(H\right)$ containing at least one element of $\mathcal{V}\left(G\right)$. For all filtering functions $f:E \to \mathbb{R}$, let $\lambda_{(G, f)}:\Delta^+ \to \mathbb{Z}$ be defined by $\lambda_{(G, f)}(u, v) = \Lambda(\iota_{(u, v)})$ where $\iota_{(u, v)}: G_u \to G_v$ is the inclusion homomorphism. Then the functions $\lambda_{(G, f)}$ are persistence functions. If the coherent sampling is stable, so are the persistence functions.
Combinatorial persistence
Coherent samplings - Clique communities
Combinatorial persistence
Coherent samplings - Clique communities
The assignment $\mathcal{C}^k$, which maps each graph $G$ to the set of its $k$-clique communities, is a stable coherent sampling.
Classical use of cliques communities:
B. Rieck, U. Fugacci, J. Lukasczyk, and H. Leitte. Clique community persistence: A topological visual analysis approa for complex networks. IEEE transactions on visualization and computer graphics, 2018.
S. Fortunato. Community detection in graphs Physics reports, 2010.
Combinatorial persistence
Property-based filters
Let $\left(G,f\right)$ be a weighted graph, with $G=(V, E)$
$F: 2^{V\cup E} \to \{true, false\}$ a property.
We call $F$-set any set $A\subseteq V\cup E$ such that $F(A) = true$.
$A\subseteq V\cup E$ is an $F$-set at level $w$
if it is an $F$-set of the subgraph $G_w$.
Combinatorial persistence
Property-based filters
We call $A\subseteq V\cup E$ a steady $F$-set
$(u, v) \in \Delta^+$ if it is an $F$-set at all levels $w$ with
$u\le w \le v$.
We call $A$ a ranging $F$-set
at $(u, v)$ if there exist levels $w\le u$ and $w'\ge v$ at which it is an $F$-set.
Let $SF_{(G, f)}(u,v)$ be the set of s-$F$-sets at $(u, v)$ and let $RF_{(G, f)}(u,v)$
be the set of r-$F$-sets at $(u, v)$.
Combinatorial persistence
Property-based filters
The functions
$$
\begin{array}{l l}
\sigma:\Delta^+\rightarrow \mathbb{R}\\
(u,v)\mapsto \left|SF_{(G, f)}(u,v)\right|
\end{array}
$$
and
$$
\begin{array}{l l}
\rho:\Delta^+\rightarrow \mathbb{R}\\
(u,v)\mapsto \left|RF_{(G, f)}(u,v)\right|
\end{array}
$$
are persistence functions.
Combinatorial persistence
Hubs
A temporary hub (t-hub) at level $u$ is a vertex of $G_u\subseteq G$ whose degree is
greater than the degree of its neighbors.
A steady hub (s-hub) at $(u, v)\in \Delta^+$ is a vertex which is a t-hub at all levels
$w$ with $u\le w \le v$.
A ranging hub (r-hub) at $(u, v)\in \Delta^+$ is a vertex such that there exist levels
$w \le u$ and $w^\prime\ge v$ at which it is a t-hub.
Combinatorial persistence
Hubs
Combinatorial persistence
Hubs
Applications
Les Miserables
Characters co-occurence
Don't you see an interactive graph? Please reload the page (Ctrl+R or command+R on mac).
Les Miserables
Characters co-occurence
Steady hubs
Ranging hubs
Les Miserables
... dealing with too many hubs?
V. Kurlin. A fast persistence-based segmentation of noisy 2D clouds with provable guarantees. Pattern recognition letters, 83:3-12, 2016.
Les Miserables
Select them!
V. Kurlin. A fast persistence-based segmentation of noisy 2D clouds with provable guarantees. Pattern recognition letters, 83:3-12, 2016.
Les Miserables
Characters co-occurence
Steady hubs
Ranging hubs
Les Miserables
Characters co-occurence
Steady hubs
Ranging hubs
Hubs in Game of Throne (books I-V)
Characters co-occurence
Don't you see an interactive graph? Please reload the page (Ctrl+R or command+R on mac).
Time-varying hubs in Game of Thrones (books I-V)
Characters co-occurence
Don't you see an interactive graph? Please reload the page (Ctrl+R or command+R on mac).
Other applications
Language and airport hubs
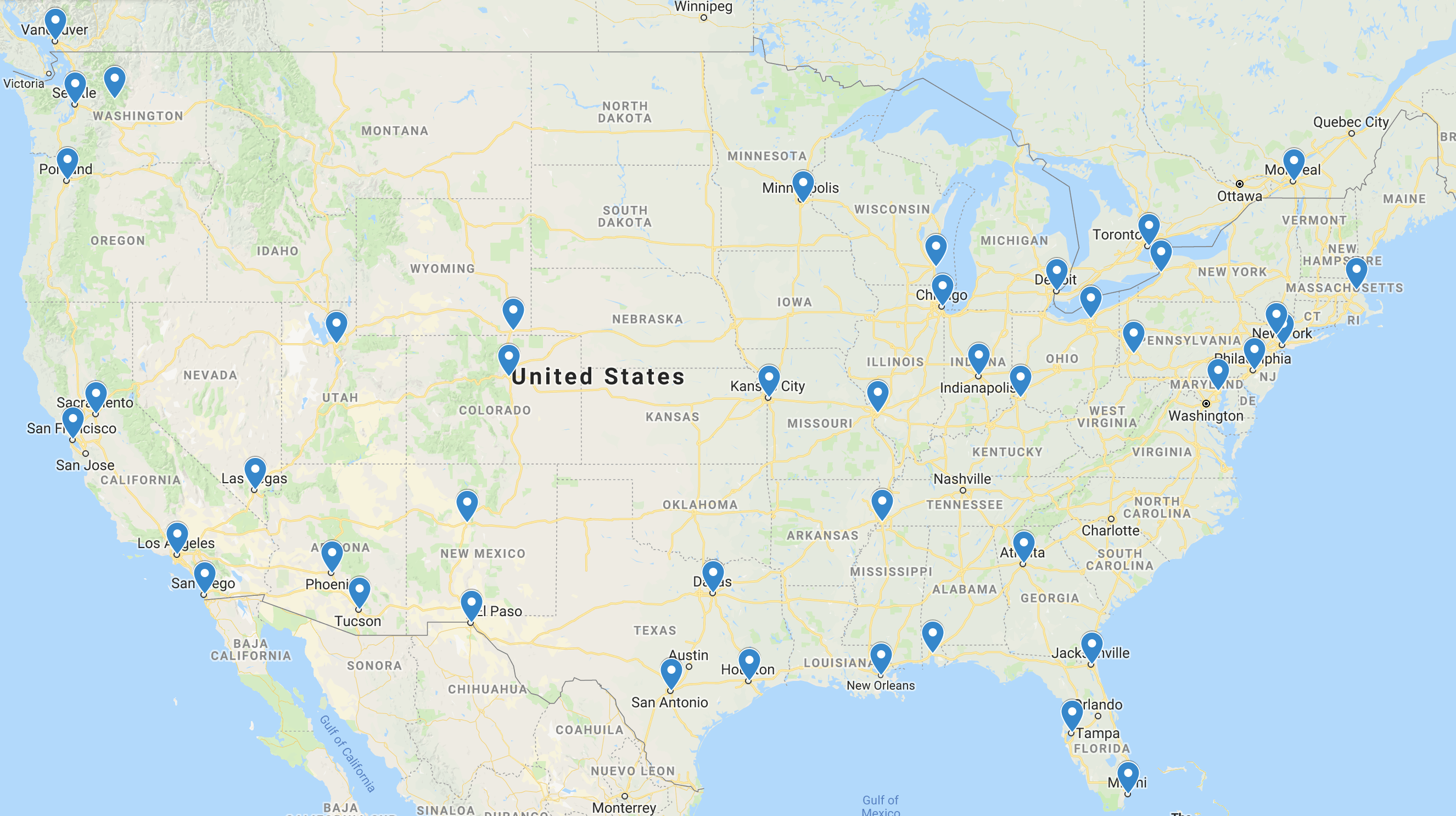
Conclusions
Persistence-based signatures of data can be generated without auxiliary topological constructions.
Coeherent samplings and property-based filters are general recipes to create persistence functions.
We are working on a categorical extension of the theory presented here for weighted graphs.
graph = pc.WeightedGraph(graph_structure)
graph.build_graph()
graph.build_filtered_subgraphs(weight_transform=opp,
sublevel=True)
graph.get_temporary_hubs_along_filtration()
graph.ranging_hubs_persistence()
graph.plot_ranging_persistence_diagram()